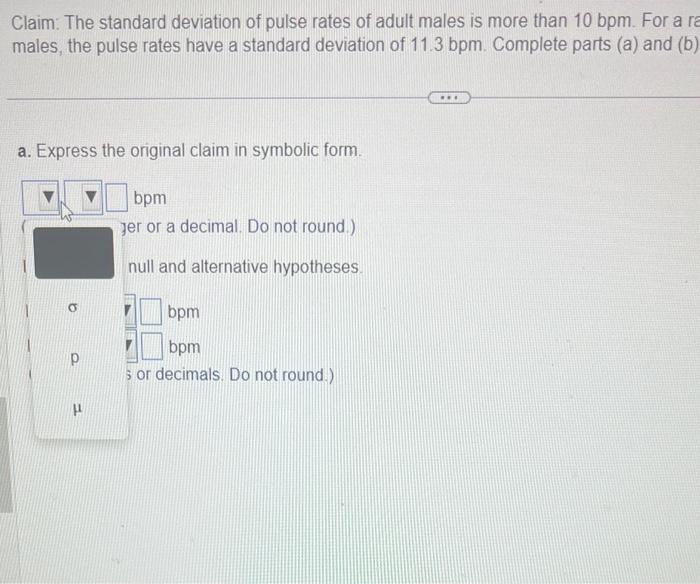
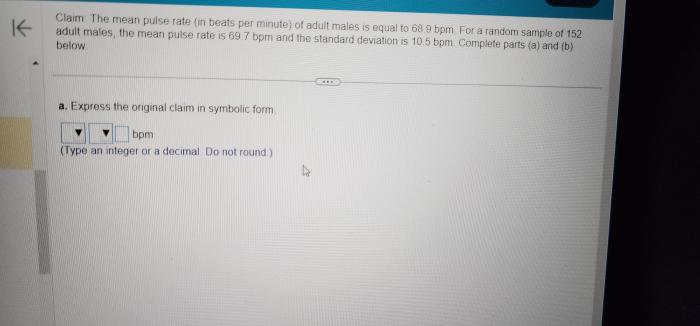
Express the original claim in symbolic form. – In the realm of logic and reasoning, the concept of expressing claims in symbolic form holds immense significance. This guide delves into the intricacies of symbolic representation, exploring its applications and limitations while providing a comprehensive overview of its essential components.
Symbolic form offers a precise and unambiguous method for representing claims, facilitating rigorous analysis and evaluation. It enables the construction of logical arguments, the identification of logical fallacies, and the exploration of complex relationships between propositions.
Symbolic Form Representation
Symbolic form is a method of expressing claims or propositions using symbols and logical operators. It allows for the precise representation of complex arguments and facilitates logical analysis.
To convert a claim into symbolic form, we use propositional variables to represent the individual claims and logical operators to connect them. For example, if we have two claims, P: “It is raining” and Q: “The grass is wet”, we can represent them symbolically as:
P: RQ: W
We can then use logical operators to combine these propositions. For example, the claim “It is raining and the grass is wet” can be represented symbolically as:
P ∧ Q
Where ∧ represents the logical operator “AND”.
Logical Operators
Logical operators are symbols used to combine propositions and specify the relationship between them. The most common logical operators are:
- AND (∧):True if both propositions are true, false otherwise.
- OR (∨):True if either proposition is true, false only if both are false.
- NOT (¬):True if the proposition is false, false if the proposition is true.
Propositional Variables
Propositional variables are symbols that represent individual claims or propositions. They are typically represented by capital letters (e.g., P, Q, R). Propositional variables allow us to break down complex arguments into their component parts and analyze their logical relationships.
For example, in the claim “If it is raining, then the grass is wet”, we can represent the propositional variables as:
P: It is rainingQ: The grass is wet
We can then express the claim symbolically as:
P → Q
Where → represents the logical operator “IF…THEN”.
Truth Tables, Express the original claim in symbolic form.
Truth tables are a tabular method of evaluating the validity of symbolic expressions. They show the truth values of the propositions for all possible combinations of truth values of the propositional variables.
For example, the truth table for the expression P ∧ Q is as follows:
| P | Q | P ∧ Q |
|---|---|---|
| T | T | T |
| T | F | F |
| F | T | F |
| F | F | F |
This table shows that the expression P ∧ Q is only true when both P and Q are true.
Applications of Symbolic Form
Symbolic form has numerous applications in various fields, including:
- Logic:Symbolic form is used to represent and analyze logical arguments and fallacies.
- Mathematics:Symbolic form is used to represent mathematical equations and proofs.
- Computer Science:Symbolic form is used in the design and analysis of computer programs.
For example, in logic, symbolic form can be used to represent and evaluate syllogisms. In mathematics, symbolic form can be used to represent and solve algebraic equations. In computer science, symbolic form can be used to represent and analyze the flow of a program.
FAQs: Express The Original Claim In Symbolic Form.
What are the benefits of using symbolic form?
Symbolic form offers several benefits, including increased precision, clarity, and the ability to identify logical relationships more easily.
How are logical operators used in symbolic form?
Logical operators, such as AND, OR, and NOT, are used to combine propositions and create more complex claims.
What is the role of propositional variables in symbolic form?
Propositional variables represent individual claims or statements, allowing for the construction of more complex symbolic expressions.
How are truth tables used in symbolic form?
Truth tables provide a systematic way to evaluate the validity of symbolic expressions by considering all possible combinations of truth values.